Lomb-Scargle ピリオドグラム(Lomb-Scargle Periodogram)法 ~Delphiでお手軽プログラミング
Lomb-Scargle ピリオドグラム(Lomb-Scargle Periodogram)法のユニット
//Lomb-Scargle ピリオドグラム(Lomb-Scargle Periodogram)
unit ULSP;
interface
uses System.SysUtils,System.Math;
type
TLSPDataSingleton=record
PastSec:Extended;//経過時間(秒)
Data:Extended; //入力信号
end;
TLSPData=array of TLSPDataSingleton;
TLSPSpecSingleton=record
Hz:Extended;
Data:Extended;
end;
TLSPSpec=array of TLSPSpecSingleton;
procedure lsp(InData:TLSPData;var OutData:TLSPSpec;
SHz,EHz,PHz:Extended);
implementation
uses Unit1;
//データ,出力データ,解析する最小周波数,解析する最大周波数,解析するステップ周波数
procedure lsp(InData:TLSPData;var OutData:TLSPSpec;
SHz,EHz,PHz:Extended);
var i,j:integer;
imax:integer;
c,s,ys1,yc1,cc1,cc2,ss1,ss2,cs1,cs2:Extended;
d,p,p_u,p_d:Extended;
w,wt:extended;
DataCt:integer;
DataSum,DataAve:extended;
sigma:Extended;
coswt,sinwt:Extended;
begin
DataCt:=Length(InData);
DataSum:=0;
for i := 0 to DataCt-1 do
begin
DataSum:=DataSum+InData[i].Data;
end;
DataAve:=DataSum/DataCt;
sigma:=0;
for i := 0 to DataCt-1 do
begin
sigma:=sigma+power(InData[i].Data-DataAve,2);
end;
imax:=floor((EHz-SHz) / PHz);
for i := 0 to imax do
begin
c:=0;
s:=0;
ys1:=0;
yc1:=0;
cc2:=0;
ss2:=0;
cs2:=0;
w:=2*pi*(SHz+PHz*i);
for j := 0 to DataCt-1 do
begin
wt:=w*InData[j].PastSec;
coswt:=cos(wt);
sinwt:=sin(wt);
c:=c+coswt;
s:=s+sinwt;
yc1:=yc1+(InData[j].Data-DataAve)*coswt;
ys1:=ys1+(InData[j].Data-DataAve)*sinwt;
cc2:=cc2+power(coswt,2);
ss2:=ss2+power(sinwt,2);
cs2:=cs2+coswt*sinwt;
end;
cc1:=cc2-c*c;
ss1:=ss2-s*s;
cs1:=cs2-c*s;
d:=cc1*ss1-cs1*cs1;
p_u:=ss1*yc1*yc1+cc1*ys1*ys1-2*cs1*yc1*ys1;
p_d:=sigma*d;
if p_d=0 then p_d:=1;
p:=p_u/p_d;
setlength(OutData,i+1);
OutData[i].Hz:=SHz+PHz*i;
OutData[i].Data:=sqrt(abs(p));
end;
end;
end.
参考URLhttps://jp.mathworks.com/help/signal/examples/spectral-analysis-of-nonuniformly-sampled-signals.html
https://qiita.com/thas_i/items/03e1e6c6d5c311de6ec6
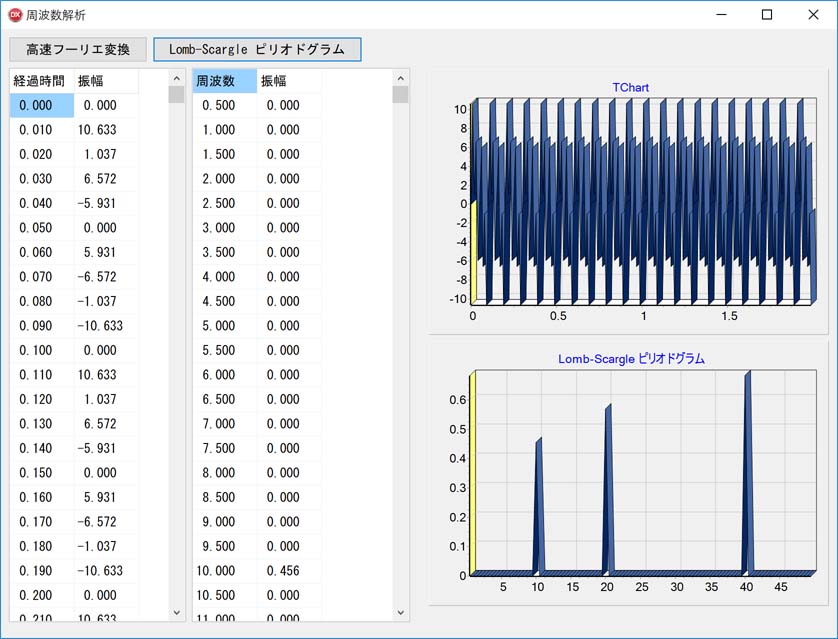
データが連続(一定間隔でデータを取得)していれば高速フーリエ変換で周波数解析ができるのですが、 一様にサンプリングされず欠損データがある場合はLomb-Scargle ピリオドグラム(Lomb-Scargle Periodogram)法を使うのがいいそうです。
Lomb-Scargle ピリオドグラム法を使ってみる
unit Unit1;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls;
type
TForm1 = class(TForm)
Button1: TButton;
Button2: TButton;
procedure Button2Click(Sender: TObject);
procedure Button1Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses ULSP,system.math;
procedure TForm1.Button2Click(Sender: TObject);
var InData:TLSPData; //入力
OutData:TLSPSpec;//出力
n,i:integer;
bs:extended; // サンプリング間隔(秒)
hz:extended; // サンプリング周波数(Hz)= 1/bs
bhz:extended;
begin
n:=200; //サンプル数
bs:=0.01;//サンプリング間隔(10ミリ秒毎のデータ)
hz:=1/bs;//サンプリング周波数(100Hz)
//テストデータの作成
setlength(InData,n);
for i := 0 to n-1 do
begin
InData[i].PastSec:= i*bs;//経過時間
InData[i].Data := 4*sin(i*bs*2*pi*10)+ //10Hz
5*sin(i*bs*2*pi*20)+ //20Hz
6*sin(i*bs*2*pi*40); //40Hz
end;
bhz:=0.5;//出力周波数間隔
LSP(InData,OutData, bhz, hz/2-bhz, bhz);
for i := 0 to length(OutData)-1 do
begin
//Format('%6.3f',[OutData[i].Hz]);
//Format('%6.3f',[OutData[i].Data]);
end;
end;
end.
上記例ではサンプリング間隔10ms(サンプリング周波数100Hz)で 振幅4の10Hz、振幅5の20Hz、振幅6の40Hzの合成データを与えています。