人工ニューラルネットワークをフルスクラッチで作成 ~Delphiソースコード集
人工ニューラルネットワーク(Artificial Neural Network)を使用する為のファイルの準備
本ページ最下部にある「UMamAnn.pas」ソースコードを、プロジェクトフォルダ内に「UMamAnn.pas」ファイルとして保存します。
ほかに必要なファイルやライブラリはありません。
TMamAnnクラスのインスタンスを作り、Trainプロシージャで学習し、Runプロシージャで学習結果をもとに結果を返します。
活性化関数はシグモイド関数だけです。
参考URL
https://atmarkit.itmedia.co.jp/ait/articles/2202/09/news027.html
Delphiを起動して新規作成を行い、必要なコンポーネントをドラッグ&ドロップする
Delphi起動⇒ファイル⇒新規作成⇒WindowsVCLアプリケーション を選択します。
TButton 2個、TMemo 1個、をフォームへドラッグ&ドロップします。
「ファイル」⇒「全て保存」でフォルダを作成して、プロジェクトとユニットを保存します。
プロジェクトフォルダ内にUMamAnn.pasファイルを配置します。
ソースコードを記述する
Button1のOnClickイベント、Button2のOnClickイベントに以下ソースコードを記述します。
unit Unit1;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls;
type
TForm1 = class(TForm)
Button1: TButton;
Button2: TButton;
Memo1: TMemo;
procedure Button1Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses UMamAnn;
procedure TForm1.Button1Click(Sender: TObject);
var Neurons:TArray<Integer>;
Ann:TMamAnn;
Inputs,OutPuts:TArray<Single>;
epoch:Integer;//繰り返し学習
begin
//排他論理和(XOR)を「回帰問題」として学習させる
Memo1.Clear;
SetLength(Neurons,3);//3層
Neurons[0]:=2;//入力層のニューロン数
Neurons[1]:=2;//中間層のニューロン数
Neurons[2]:=1;//出力層のニューロン数
SetLength(Inputs,2); //入力層データ
SetLength(Outputs,1);//出力層データ
Ann:=TMamAnn.Create(Neurons);
try
//10000回繰り返し学習させる
for epoch := 1 to 10000 do
begin
//0 XOR 0 = 0を学習させる
Inputs[0]:=0;
Inputs[1]:=0;
OutPuts[0]:= Trunc(Inputs[0]) XOR Trunc(Inputs[1]);
Ann.Train(Inputs,Outputs);//学習
//0 XOR 1 = 1を学習させる
Inputs[0]:=0;
Inputs[1]:=1;
OutPuts[0]:= Trunc(Inputs[0]) XOR Trunc(Inputs[1]);
Ann.Train(Inputs,Outputs);//学習
//1 XOR 0 = 1を学習させる
Inputs[0]:=1;
Inputs[1]:=0;
OutPuts[0]:= Trunc(Inputs[0]) XOR Trunc(Inputs[1]);
Ann.Train(Inputs,Outputs);//学習
//1 XOR 1 = 0を学習させる
Inputs[0]:=1;
Inputs[1]:=1;
OutPuts[0]:= Trunc(Inputs[0]) XOR Trunc(Inputs[1]);
Ann.Train(Inputs,Outputs);//学習
end;
//学習結果をファイルに保存する
//Ann.SaveToFile('xor.net');
Memo1.Lines.Add('排他論理和(XOR)を「回帰問題」として学習');
//0 XOR 0 がいくつかAIに聞く
Inputs[0]:=0;
Inputs[1]:=0;
Ann.Run(Inputs,Outputs);
Memo1.Lines.Add(
Format('%1.0f XOR %1.0f = %1.0f',[Inputs[0],Inputs[1],Outputs[0]])
);
//0 XOR 1 がいくつかAIに聞く
Inputs[0]:=0;
Inputs[1]:=1;
Ann.Run(Inputs,Outputs);
Memo1.Lines.Add(
Format('%1.0f XOR %1.0f = %1.0f',[Inputs[0],Inputs[1],Outputs[0]])
);
//1 XOR 0 がいくつかAIに聞く
Inputs[0]:=1;
Inputs[1]:=0;
Ann.Run(Inputs,Outputs);
Memo1.Lines.Add(
Format('%1.0f XOR %1.0f = %1.0f',[Inputs[0],Inputs[1],Outputs[0]])
);
//1 XOR 1 がいくつかAIに聞く
Inputs[0]:=1;
Inputs[1]:=1;
Ann.Run(Inputs,Outputs);
Memo1.Lines.Add(
Format('%1.0f XOR %1.0f = %1.0f',[Inputs[0],Inputs[1],Outputs[0]])
);
finally
Ann.Free;
end;
end;
procedure TForm1.Button2Click(Sender: TObject);
var Neurons:TArray<Integer>;
Ann:TMamAnn;
Inputs,OutPuts:TArray<Single>;
epoch:Integer;//繰り返し学習
begin
//排他論理和(XOR)を「分類問題」として学習させる
Memo1.Clear;
SetLength(Neurons,3);//3層
Neurons[0]:=2;//入力層のニューロン数
Neurons[1]:=2;//中間層のニューロン数
Neurons[2]:=2;//出力層のニューロン数
SetLength(Inputs,2); //入力層データ
SetLength(Outputs,2);//出力層データ
Ann:=TMamAnn.Create(Neurons);
try
//10000回繰り返し学習させる
for epoch := 1 to 10000 do
begin
//0 XOR 0 = 0を学習させる
Inputs[0]:=0;
Inputs[1]:=0;
OutPuts[0]:=1;//答えは「0」か
OutPuts[1]:=0;//答えは「1」か
Ann.Train(Inputs,Outputs);//学習
//0 XOR 1 = 1を学習させる
Inputs[0]:=0;
Inputs[1]:=1;
OutPuts[0]:=0;//答えは「0」か
OutPuts[1]:=1;//答えは「1」か
Ann.Train(Inputs,Outputs);//学習
//1 XOR 0 = 1を学習させる
Inputs[0]:=1;
Inputs[1]:=0;
OutPuts[0]:=0;//答えは「0」か
OutPuts[1]:=1;//答えは「1」か
Ann.Train(Inputs,Outputs);//学習
//1 XOR 1 = 0を学習させる
Inputs[0]:=1;
Inputs[1]:=1;
OutPuts[0]:=1;//答えは「0」か
OutPuts[1]:=0;//答えは「1」か
Ann.Train(Inputs,Outputs);//学習
end;
//学習結果をファイルに保存する
//Ann.SaveToFile('xor.net');
Memo1.Lines.Add('排他論理和(XOR)を「分類問題」として0か1かを学習');
//0 XOR 0 が「0」か「1」のどちらかをAIに聞く
Inputs[0]:=0;
Inputs[1]:=0;
Ann.Run(Inputs,Outputs);
Memo1.Lines.Add(
Format('%1.0f XOR %1.0fが 0の確率%3.0f%%、1の確率%3.0f%%',
[Inputs[0],Inputs[1],Outputs[0]*100,Outputs[1]*100])
);
//0 XOR 1 がいくつかAIに聞く
Inputs[0]:=0;
Inputs[1]:=1;
Ann.Run(Inputs,Outputs);
Memo1.Lines.Add(
Format('%1.0f XOR %1.0fが 0の確率%3.0f%%、1の確率%3.0f%%',
[Inputs[0],Inputs[1],Outputs[0]*100,Outputs[1]*100])
);
//1 XOR 0 がいくつかAIに聞く
Inputs[0]:=1;
Inputs[1]:=0;
Ann.Run(Inputs,Outputs);
Memo1.Lines.Add(
Format('%1.0f XOR %1.0fが 0の確率%3.0f%%、1の確率%3.0f%%',
[Inputs[0],Inputs[1],Outputs[0]*100,Outputs[1]*100])
);
//1 XOR 1 がいくつかAIに聞く
Inputs[0]:=1;
Inputs[1]:=1;
Ann.Run(Inputs,Outputs);
Memo1.Lines.Add(
Format('%1.0f XOR %1.0fが 0の確率%3.0f%%、1の確率%3.0f%%',
[Inputs[0],Inputs[1],Outputs[0]*100,Outputs[1]*100])
);
finally
Ann.Free;
end;
end;
end.
実行する
実行ボタンを押して実行します。(デバッグ実行でもOK)
Button1をクリックすると、排他論理和(XOR)を「回帰問題」として学習し、AIが排他論理和の答えを返します。
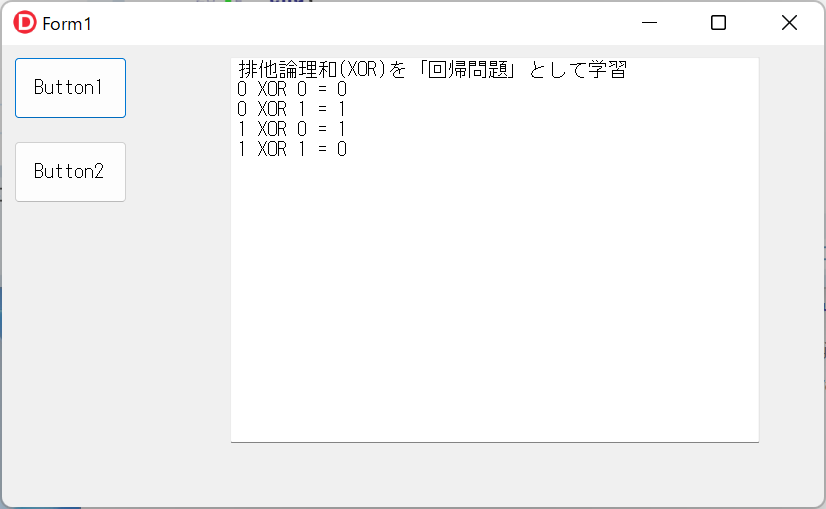
Button2をクリックすると、排他論理和(XOR)を「分類問題」として学習し、AIが排他論理和の答えを返します。
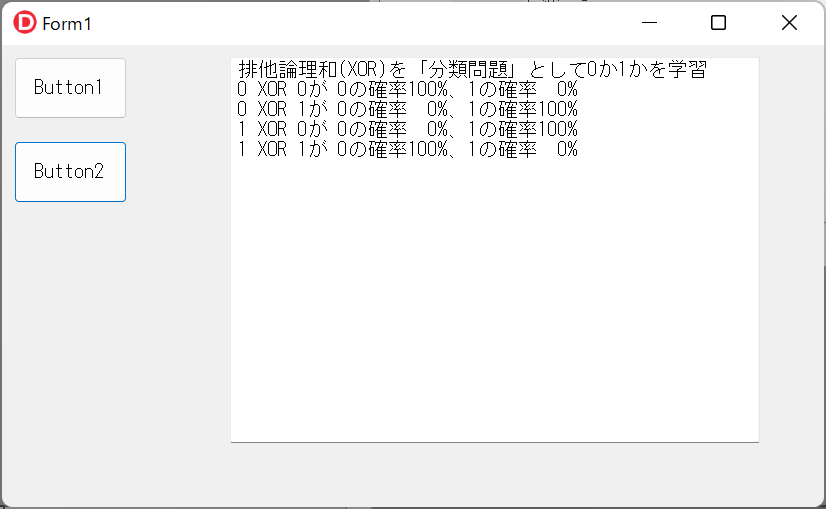
UMamAnn.pasソースコード
unit UMamAnn;
interface
uses System.Math,System.Classes,System.SysUtils;
{
人工ニューラルネットワーク(Artificial Neural Network)クラスのライブラリ
活性化関数
TMamActivationFunc.Sigmoid指定時
中間層はシグモイド関数、出力層は恒等関数を使用
TMamActivationFunc.ReLU指定時
中間層はReLU関数、出力層はシグモイド関数を使用
◎=入力層のニューロン
●=中間層のニューロン
○=出力層のニューロン
■=重み
▼=バイアス
値 重み バイアス
fSum fWeight fBias
fOut fGradsW fGradsB
i0 ◎◎
j0j1 j0 j1 j2 j0j1j2
i0■■ ■■ ■■ i0▼▼▼
k0k1 k0k1 k0k1
i1 ●●●
j0j1j2 j0 j1 j0j1
i1■■■ ■■■ i1▼▼
k0k1k2 k0k1k2
i2 ●●
j0j1 j0 j1 j0j1
i2■■ ■■ i2▼▼
k0k1 k0k1
i3 ○○
j0j1
}
type
TMamActivationFunc=(Sigmoid,ReLU);
TMamAnn=class(TObject)
private
fSum:TArray<TArray<single>>;//各層の値(重み付線形和)
fOut:TArray<TArray<single>>;//各層の値(重み付線形和の活性化関数適用後)
fLayerCount:Integer;//層の数
fNeuronCountInLayers:TArray<Integer>;//各層のニューロン数
fLearningRate:single;//学習率
fLoss:Single;//損失値(累計2乗誤差)
fTrainCount:Integer;//学習回数
fBias:TArray<TArray<single>>;//バイアス
fWeight:TArray<TArray<TArray<single>>>;//重みづけ(-1~1)
fActivationFunc:TMamActivationFunc;
procedure ForwardProp(Inputs:TArray<Single>);//順伝播
procedure BackProp(Outputs:TArray<Single>); //逆伝播とパラメータ更新
function Sigmoid(x:Single):Single; //シグモイド
function SigmoidDerivative(x:single):single; //シグモイドの導関数
function ReLU(x: single): single;
function ReLUDerivative(x: single): single;
function GetLearningRate():Single;
procedure SetLearningRate(LearningRage:Single);
public
constructor Create(
NeuronCountInLayers:TArray<Integer>;LerningRate:Single=0.2;
ActivationFunc:TMamActivationFunc=TMamActivationFunc.Sigmoid
);overload;
constructor Create(Filename:String);overload;
//学習
procedure Train(Inputs,Outputs: TArray<Single>);
//予測の実行
procedure Run(Inputs:TArray<Single>;out Outputs:TArray<Single>);
//MSE(平均二乗誤差)出力
function GetMSE():Single;
destructor Destroy; override;
procedure SaveToFile(FileName:String);
procedure LoadFromFile(FileName:String);
property LearningRate:Single read GetLearningRate write SetLearningRate;
end;
implementation
{ TMamAnn }
function TMamAnn.ReLU(x: single): single;
begin
if x>0 then result:=x else result:=0;
end;
function TMamAnn.ReLUDerivative(x: single): single;
begin
if x>0 then result:=1 else result:=0;
end;
procedure TMamAnn.BackProp(Outputs:TArray<Single>);
var i,j,k:Integer;
loss_der:single;
back_error:TArray<Single>;
active_der:single;
delta:single;
sum_der_w,sum_der_x:TArray<Single>;
sum_der_b:Single;
layer_grads_x:TArray<Single>;
begin
//逆伝播とパラメータ更新
SetLength(layer_grads_x,0);
for i := (fLayerCount-1) downto 1 do
begin
if i=(fLayerCount-1) then
begin
//出力層の場合
SetLength(back_error,Length(Outputs));
for j := Low(Outputs) to High(Outputs) do
begin
loss_der:=fOut[i][j]-Outputs[j];
back_error[j]:=loss_der;
end;
end
else
begin
//隠れ層(次の層への入力の偏微分係数)
//最後に追加された入力の勾配(layer_grads_x)をback_errorに入れる
SetLength(back_error,Length(layer_grads_x));
Move(
layer_grads_x[0],
back_error[0],
SizeOf(layer_grads_x[0])*Length(layer_grads_x)
);
end;
for j := Low(fSum[i]) to High(fSum[i]) do
begin
if i=(fLayerCount-1) then
begin
//出力層の場合
if fActivationFunc=TMamActivationFunc.Sigmoid then
//恒等関数の導関数
active_der:=1.0
else
//シグモイド関数の導関数
active_der:=SigmoidDerivative(fSum[i][j]);
end
else
begin
//出力層以外の場合
if fActivationFunc=TMamActivationFunc.Sigmoid then
//シグモイド関数の導関数
active_der:=SigmoidDerivative(fSum[i][j])
else
//ReLU関数の導関数
active_der:=ReLUDerivative(fSum[i][j]);
end;
//fOut[i-1]配列をsum_der_wにコピー
SetLength(sum_der_w,Length(fOut[i-1]));
Move(
fOut[i-1][0],
sum_der_w[0],
Sizeof(fOut[i-1][0])*Length(fOut[i-1])
);
sum_der_b:=1.0;
//fWeight[i-1][j]配列をsum_der_xにコピー
SetLength(sum_der_x,Length(fWeight[i-1][j]));
Move(
fWeight[i-1][j][0], sum_der_x[0],
Sizeof(fWeight[i-1][j][0])*Length(fWeight[i-1][j])
);
//勾配を計算
delta:=back_error[j]*active_der;
//勾配からバイアス計算してバイアスを更新する
fBias[i-1][j]:=fBias[i-1][j]-delta*sum_der_b*fLearningRate;
if j=0 then SetLength(layer_grads_x,Length(sum_der_w));
//重みと入力
for k := Low(sum_der_w) to High(sum_der_w) do
begin
//勾配から重みの計算を行い重みを更新する
fWeight[i-1][j][k]:=
fWeight[i-1][j][k]-delta*sum_der_w[k]*fLearningRate;
//入力は各ノードから前のノードに接続する全ての入力を合計する
if j=0 then
begin
layer_grads_x[k]:=delta *sum_der_x[k];
end
else
begin
layer_grads_x[k]:=layer_grads_x[k]+delta *sum_der_x[k];
end;
end;
end;
end;
end;
constructor TMamAnn.Create(
NeuronCountInLayers:TArray<Integer>;LerningRate: Single=0.2;
ActivationFunc:TMamActivationFunc=TMamActivationFunc.Sigmoid);
var i,j,k,num:Integer;
scale:Single;
begin
fLearningRate:=LerningRate;
if fLearningRate>0.999 then fLearningRate:=0.999;
if fLearningRate<0.001 then fLearningRate:=0.001;
//Sigmoid または ReLU
fActivationFunc:=ActivationFunc;
fLoss:=0;
fTrainCount:=0;
fLayerCount:=Length(NeuronCountInLayers);
SetLength(fNeuronCountInLayers,fLayerCount);
Move(
NeuronCountInLayers[0],
fNeuronCountInLayers[0],
SizeOf(NeuronCountInLayers[0])*Length(NeuronCountInLayers)
);
Randomize;
//値初期化
SetLength(fOut,fLayerCount);
SetLength(fSum,fLayerCount);
for i := Low(fOut) to High(fOut) do
begin
num:=fNeuronCountInLayers[i];
SetLength(fOut[i],num);
SetLength(fSum[i],num);
end;
//バイアス初期化(0にする)
SetLength(fBias,fLayerCount-1);
for i := Low(fBias) to High(fBias) do
begin
SetLength(fBias[i],fNeuronCountInLayers[i+1]);
for j := Low(fBias[i]) to High(fBias[i]) do
fBias[i][j]:=0;
end;
//重みづけ初期化
SetLength(fWeight,fLayerCount-1);
for i := Low(fWeight) to High(fWeight) do
begin
SetLength(fWeight[i],fNeuronCountInLayers[i+1]);
for j := Low(fWeight[i]) to High(fWeight[i]) do
begin
SetLength(fWeight[i][j],Length(fOut[i]));
if i=High(fWeight) then
begin
scale:=1/sqrt(Length(fWeight[i][j]));
end
else
begin
//乱数だけだと永遠にMSEが収束しない場合がある(1/20回くらい)
if fActivationFunc=TMamActivationFunc.Sigmoid then
//平均0、1/√nのガウス分布乱数
scale:=1/sqrt(Length(fWeight[i][j]))
else
//平均0、√(2/(n1+n2))のガウス分布乱数
scale:=sqrt(2/Length(fWeight[i][j]))
end;
for k := Low(fWeight[i][j]) to High(fWeight[i][j]) do
begin
if (fActivationFunc=TMamActivationFunc.Sigmoid) then
begin
if k=Low(fWeight[i][j]) then
fWeight[i][j][k]:=scale
else if k=High(fWeight[i][j]) then
fWeight[i][j][k]:=-scale
else
fWeight[i][j][k]:=RandG(0,scale);
end
else
begin
if (i=High(fWeight[i])) then
begin
if k=Low(fWeight[i][j]) then
fWeight[i][j][k]:=scale
else if k=High(fWeight[i][j]) then
fWeight[i][j][k]:=-scale
else
fWeight[i][j][k]:=RandG(0,scale);
end
else
if k=Low(fWeight[i][j]) then
fWeight[i][j][k]:=scale*3.5
else if k=High(fWeight[i][j]) then
fWeight[i][j][k]:=-scale*0.5
else
fWeight[i][j][k]:=RandG(0,scale);
end;
end;
end;
end;
end;
constructor TMamAnn.Create(Filename: String);
begin
Randomize;
Self.LoadFromFile(Filename);
end;
destructor TMamAnn.Destroy;
begin
inherited;
end;
procedure TMamAnn.ForwardProp(Inputs: TArray<Single>);
var i,j,k:Integer;
ww:Single;
begin //順伝播
//入力層に入力値を入れる
Move(Inputs[0],fSum[0][0],SizeOf(Inputs[0])*Length(Inputs));
Move(Inputs[0],fOut[0][0],SizeOf(Inputs[0])*Length(Inputs));
//入力層から中間層から出力層まで計算する
for i := Low(fWeight) to High(fWeight) do
begin
for j := Low(fWeight[i]) to High(fWeight[i]) do
begin
//fSum[i+1][j]:=
// fOut[i][ 0]*fWeight[i][j][ 0]+
// fOut[i][ 1]*fWeight[i][j][ 1]+
// fOut[i][...]*fWeight[i][j][...]+fBias[i][j];
//fOut[i*1][j]:=活性化関数(fSum[i+1][j]);
ww:=fBias[i][j];
for k := Low(fWeight[i][j]) to High(fWeight[i][j]) do
begin
ww:=ww+fOut[i][k]*fWeight[i][j][k];
end;
fSum[i+1][j]:=ww;
if i=(fLayerCount-2) then
begin
//出力層の場合
if fActivationFunc=TMamActivationFunc.Sigmoid then
begin
//恒等関数
ww:=ww;
end
else
begin
//シグモイド関数
ww:=Sigmoid(ww);
end;
end
else
begin
//出力層以外の場合
if fActivationFunc=TMamActivationFunc.Sigmoid then
//シグモイド関数
ww:=Sigmoid(ww)
else
//ReLU関数
ww:=ReLU(ww);
end;
fOut[i+1][j]:=ww;
end;
end;
end;
function TMamAnn.GetLearningRate: Single;
begin
result:=fLearningRate;
end;
function TMamAnn.GetMSE: Single;
begin //MSE(平均二乗誤差)出力
if fTrainCount>0 then
result:=fLoss/fTrainCount
else
result:=0;
end;
procedure TMamAnn.LoadFromFile(FileName: String);
var strm:TMemoryStream;
i,j,k:Integer;
act:Integer;
begin //ファイルからの読み込み
strm:=TMemoryStream.Create;
try
strm.LoadFromFile(FileName);
strm.Position:=0;
//活性化関数読み込み
strm.ReadData(act);
if act=0 then
fActivationFunc:=TMamActivationFunc.Sigmoid
else
fActivationFunc:=TMamActivationFunc.ReLU;
//層数読み込み
strm.ReadData(fLayerCount);
//層ごとのニューロン数読み込み
setLength(fNeuronCountInLayers,fLayerCount);
for i := 0 to fLayerCount-1 do
strm.ReadData(fNeuronCountInLayers[i]);
//学習率の読み込み
strm.ReadData(fLearningRate);
//損失値(累計2乗誤差)読み込み
strm.ReadData(fLoss);
//学習回数読み込み
strm.ReadData(fTrainCount);
//fSum,fOutの準備
SetLength(fSum,fLayerCount);
SetLength(fOut,fLayerCount);
for i := 0 to fLayerCount-1 do
begin
SetLength(fSum[i],fNeuronCountInLayers[i]);
SetLength(fOut[i],fNeuronCountInLayers[i]);
end;
//バイアス読み込み
SetLength(fBias,fLayerCount-1);
for i := Low(fBias) to High(fBias) do
begin
SetLength(fBias[i],fNeuronCountInLayers[i+1]);
for j := Low(fBias[i]) to High(fBias[i]) do
begin
strm.ReadData(fBias[i][j]);
end;
end;
//重み読み込み
SetLength(fWeight,fLayerCount-1);
for i := Low(fWeight) to High(fWeight) do
begin
SetLength(fWeight[i],fNeuronCountInLayers[i+1]);
for j := Low(fWeight[i]) to High(fWeight[i]) do
begin
SetLength(fWeight[i][j],fNeuronCountInLayers[i]);
for k := Low(fWeight[i][j]) to High(fWeight[i][j]) do
begin
strm.ReadData(fWeight[i][j][k]);
end;
end;
end;
finally
strm.Free;
end;
end;
procedure TMamAnn.Run(Inputs: TArray<Single>; out Outputs: TArray<Single>);
begin //予測の実行
ForwardProp(Inputs);
//出力層の値のコピー
SetLength(Outputs,Length(fOut[High(fOut)]));
Move(
fOut[High(fOut)][0],
Outputs[0],
SizeOf(fOut[High(fOut)][0])*Length(fOut[High(fOut)])
);
end;
procedure TMamAnn.SaveToFile(FileName: String);
var strm:TMemoryStream;
i,j,k:Integer;
act:Integer;
begin //バイナリで保存する
strm:=TMemoryStream.Create();
try
//活性化関数保存
if fActivationFunc=TMamActivationFunc.Sigmoid then
act:=0
else
act:=1;
strm.WriteData(act);
//層数保存
strm.WriteData(fLayerCount);
//層ごとのニューロン数保存
for i := Low(fNeuronCountInLayers) to High(fNeuronCountInLayers) do
strm.WriteData(fNeuronCountInLayers[i]);
//学習率保存
strm.WriteData(fLearningRate);
//損失値(累計2乗誤差)保存
strm.WriteData(fLoss);
//学習回数保存
strm.WriteData(fTrainCount);
//バイアス保存
for i := Low(fBias) to High(fBias) do
for j := Low(fBias[i]) to High(fBias[i]) do
strm.WriteData(fBias[i][j]);
//重み保存
for i := Low(fWeight) to High(fWeight) do
for j := Low(fWeight[i]) to High(fWeight[i]) do
for k := Low(fWeight[i][j]) to High(fWeight[i][j]) do
strm.WriteData(fWeight[i][j][k]);
strm.SaveToFile(FileName);
finally
strm.Free;
end;
end;
procedure TMamAnn.SetLearningRate(LearningRage:Single);
begin
if LearningRate>0.999 then LearningRate:=0.999;
if LearningRate<0.001 then LearningRate:=0.001;
fLearningRate:=LearningRate;
end;
function TMamAnn.Sigmoid(x: Single): Single;
begin //シグモイド関数
result:=1.0/(1.0+system.exp(-x))
end;
function TMamAnn.SigmoidDerivative(x:single): single;
begin //シグモイド関数の微分関数
result:=Sigmoid(x);
result:=result*(1.0-result);
end;
procedure TMamAnn.Train(Inputs, Outputs: Tarray<Single>);
var j:Integer;
sub:Single;
begin //学習
//順伝播
ForwardProp(Inputs);
//逆伝播
BackProp(Outputs);
//MSE(平均二乗誤差)の為に累計2乗誤差計算
for j := Low(Outputs) to High(Outputs) do
begin
inc(fTrainCount);
sub:=fOut[High(fOut)][j]-Outputs[j];
fLoss:=fLoss+sub*sub;
end;
end;
end.
(64Bitコンパイル用)UMamAnn.pasソースコード
unit UMamAnn;
interface
uses System.Math,System.Classes,System.SysUtils,winapi.windows;
{
人工ニューラルネットワーク(Artificial Neural Network)クラスのライブラリ
活性化関数
TMamActivationFunc.Sigmoid指定時
中間層はシグモイド関数、出力層は恒等関数を使用します
TMamActivationFunc.ReLU指定時
中間層はReLU関数、出力層はシグモイド関数を使用します
◎=入力層のニューロン
●=中間層のニューロン
○=出力層のニューロン
■=重み
▼=バイアス
値 重み バイアス
fSum fWeight fBias
fOut fGradsW fGradsB
i0 ◎◎
j0j1 j0 j1 j2 j0j1j2
i0■■ ■■ ■■ i0▼▼▼
k0k1 k0k1 k0k1
i1 ●●●
j0j1j2 j0 j1 j0j1
i1■■■ ■■■ i1▼▼
k0k1k2 k0k1k2
i2 ●●
j0j1 j0 j1 j0j1
i2■■ ■■ i2▼▼
k0k1 k0k1
i3 ○○
j0j1
}
type
TMamActivationFunc=(Sigmoid,ReLU);
TMamAnn=class(TObject)
private
fSum:TArray<TArray<single>>;//各層の値(重み付線形和)
fOut:TArray<TArray<single>>;//各層の値(重み付線形和の活性化関数適用後)
fLayerCount:Integer;//層の数
fNeuronCountInLayers:TArray<Integer>;//各層のニューロン数
fLearningRate:single;//学習率
fLoss:Single;//損失値(累計2乗誤差)
fTrainCount:Integer;//学習回数
fBias:TArray<TArray<single>>;//バイアス
fWeight:TArray<TArray<TArray<single>>>;//重みづけ(-1~1)
fActivationFunc:TMamActivationFunc;
procedure ForwardProp(Inputs:TArray<Single>);//順伝播
procedure BackProp(Outputs:TArray<Single>); //逆伝播とパラメータ更新
function Sigmoid(x:Single):Single; //シグモイド
function SigmoidDerivative(x:single):single; //シグモイドの導関数
function ReLU(x: single): single;
function ReLUDerivative(x: single): single;
function GetLearningRate():Single;
procedure SetLearningRate(LearningRage:Single);
public
constructor Create(
NeuronCountInLayers:TArray<Integer>;LerningRate:Single=0.2;
ActivationFunc:TMamActivationFunc=TMamActivationFunc.Sigmoid
);overload;
constructor Create(Filename:String);overload;
//学習
procedure Train(Inputs,Outputs: TArray<Single>);
//予測の実行
procedure Run(Inputs:TArray<Single>;out Outputs:TArray<Single>);
//MSE(平均二乗誤差)出力
function GetMSE():Single;
destructor Destroy; override;
procedure SaveToFile(FileName:String);
procedure LoadFromFile(FileName:String);
property LearningRate:Single read GetLearningRate write SetLearningRate;
end;
implementation
//SSEで同時4つの浮動小数点演算を行う pD = pD + pS*coff4
procedure coffSum4(var pD, pS, coff4: single);
asm // RCX RDX R8
MOVUPS XMM0, [R8] //XMM0=coff4[0..3]
MOVUPS XMM1, [RDX] //XMM1=pS[0..3]
MOVUPS XMM2, [RCX] //XMM2=pD[0..3]
MULPS XMM1, XMM0 //XMM1=XMM1*XMM0(pS*coff4)
ADDPS XMM2, XMM1 //XMM2=XMM2+XMM1
MOVUPS [RCX],XMM2 //pD=XMM2
end;
procedure coffSum16(var pD, pS, coff4: single);
asm // RCX RDX R8
MOVUPS XMM0, [R8] //XMM0=coff4[0..3]
MOVUPS XMM1, [RDX] //XMM1=pS[0..3]
MOVUPS XMM2, [RCX] //XMM2=pD[0..3]
MULPS XMM1, XMM0 //XMM1=XMM1*XMM0(pS*coff4)
ADDPS XMM2, XMM1 //XMM2=XMM2+XMM1
MOVUPS [RCX],XMM2 //pD[0..3]=XMM2
MOVUPS XMM1, [RDX+16] //XMM1=pS[4..7]
MOVUPS XMM2, [RCX+16] //XMM2=pD[4..7]
MULPS XMM1, XMM0 //XMM1=XMM1*XMM0(pS*coff4)
ADDPS XMM2, XMM1 //XMM2=XMM2+XMM1
MOVUPS [RCX+16],XMM2 //pD[4..7]=XMM2
MOVUPS XMM1, [RDX+32] //XMM1=pS[8..11]
MOVUPS XMM2, [RCX+32] //XMM2=pD[8..11]
MULPS XMM1, XMM0 //XMM1=XMM1*XMM0(pS*coff4)
ADDPS XMM2, XMM1 //XMM2=XMM2+XMM
MOVUPS [RCX+32],XMM2 //pD[8..11]=XMM2
MOVUPS XMM1, [RDX+48] //XMM1=pS[12..15]
MOVUPS XMM2, [RCX+48] //XMM2=pD[12..15]
MULPS XMM1, XMM0 //XMM1=XMM1*XMM0(pS*coff4)
ADDPS XMM2, XMM1 //XMM2=XMM2+XMM
MOVUPS [RCX+48],XMM2 //pD[12..15]=XMM2
end;
procedure AVXcoffSum(var arD, arS: single; const coff: single; Count: integer);
var Coff4: array[0..3] of single; //SSE命令の為の4word(16byte)の入れ物
pD, pS: ^single;
i: integer;
begin
pD := @arD;
pS := @arS;
for i := 0 to High(Coff4) do coff4[i] := coff;
while Count >= 16 do //SSE命令はWin64なら必須だから4個一度に計算可能
begin
coffSum16(pD^, pS^, coff4[0]);
Inc(pD, 16);
Inc(pS, 16);
Dec(Count, 16);
end;
while Count >= 4 do //SSE命令はWin64なら必須だから4個一度に計算可能
begin
coffSum4(pD^, pS^,coff4[0]);
Inc(pD, 4);
Inc(pS, 4);
Dec(Count, 4);
end;
while Count > 0 do //残りは最大3個で普通に計算
begin
pD^ := pD^ + coff * pS^;
Inc(pD);
Inc(pS);
Dec(Count, 1);
end;
end;
//SSEで同時4つの浮動小数点演算を行う coff4[0]=SUM(pD*pS)
//ww:=ww+fOut[i][k]*fWeight[i][j][k];
procedure MulSum4(var pD, pS, coff4: single);
asm // RCX RDX R8
MOVUPS XMM1, [RDX] //XMM1=pS[0..3]
MOVUPS XMM2, [RCX] //XMM2=pD[0..3]
DPPS XMM2, XMM1,$f1 //XMM2=SUM(XMM2*XMM1)
MOVUPS [R8],XMM2 //conn4=XMM2
end;
function MulAdd(var arD, arS: single; Count: integer):single;
var Coff4: array[0..3] of single; //SSE命令の為の4word(16byte)の入れ物
pD, pS: ^single;
begin
pD := @arD;
pS := @arS;
//ZeroMemory(@Coff4[0],Length(Coff4)*Sizeof(Coff4[0]));
result:=0;
while Count >= 4 do //SSE命令はWin64なら必須だから4個一度に計算可能
begin
MulSum4(pD^, pS^,coff4[0]);
result:=result+coff4[0];
Inc(pD, 4);
Inc(pS, 4);
Dec(Count, 4);
end;
while Count > 0 do //残りは最大3個で普通に計算
begin
result := result+ pD^ * pS^;
Inc(pD);
Inc(pS);
Dec(Count, 1);
end;
end;
//SSEで同時4つの浮動小数点演算を行う layer_grads_x[k]:=sum_der_x[k]*delta
procedure Mul4(var pD, pS, coff4: single);
asm // RCX RDX R8
MOVUPS XMM0, [R8] //XMM0=coff4[0..3]
MOVUPS XMM1, [RDX] //XMM1=pS[0..3]
MULPS XMM1, XMM0 //XMM1=XMM1*XMM0(pS*coff4)
MOVUPS [RCX],XMM1 //pD = XMM1
end;
procedure Mul(var arD, arS: single; const coff:Single; Count: integer);
var Coff4: array[0..3] of single; //SSE命令の為の4word(16byte)の入れ物
pD, pS: ^single;
i:Integer;
begin
pD := @arD;
pS := @arS;
for i := 0 to High(Coff4) do coff4[i] := coff;
while Count >= 4 do //SSE命令はWin64なら必須だから4個一度に計算可能
begin
Mul4(pD^, pS^,coff4[0]);
Inc(pD, 4);
Inc(pS, 4);
Dec(Count, 4);
end;
while Count > 0 do //残りは最大3個で普通に計算
begin
pD^ := coff * pS^;
Inc(pD);
Inc(pS);
Dec(Count, 1);
end;
end;
//SSEで同時4つの浮動小数点演算を行う back_error[j]:=fOut[i][j]-Outputs[j]
procedure SUBPS4(var pD, pS, pC: single);
asm // RCX RDX R8
MOVUPS XMM0, [R8] //XMM0=pC[0..3]
MOVUPS XMM1, [RDX] //XMM1=pS[0..3]
SUBPS XMM1, XMM0 //XMM1=XMM1-XMM0
MOVUPS [RCX],XMM1 //pD=XMM1
end;
procedure SUBPS(var arD, arS, arC: single; Count: integer);
var
pD, pS, pC: ^single;
i:Integer;
begin
pD := @arD;
pS := @arS;
pC := @arC;
while Count >= 4 do //SSE命令はWin64なら必須だから4個一度に計算可能
begin
SUBPS4(pD^, pS^, pC^);
Inc(pD, 4);
Inc(pS, 4);
Inc(pC, 4);
Dec(Count, 4);
end;
while Count > 0 do //残りは最大3個で普通に計算
begin
pD^ := pS^ - pC^;
Inc(pD);
Inc(pS);
Inc(pC);
Dec(Count, 1);
end;
end;
{ TMamAnn }
function TMamAnn.ReLU(x: single): single;
begin
if x>0 then result:=x else result:=0;
end;
function TMamAnn.ReLUDerivative(x: single): single;
begin
if x>0 then result:=1 else result:=0;
end;
procedure TMamAnn.BackProp(Outputs:TArray<Single>);
var i,j{,k}:Integer;
//loss_der:single;
back_error:TArray<Single>;
active_der:single;
delta:single;
sum_der_w,sum_der_x:TArray<Single>;
sum_der_b:Single;
layer_grads_x:TArray<Single>;
begin
//逆伝播とパラメータ更新
SetLength(layer_grads_x,0);
for i := (fLayerCount-1) downto 1 do
begin
if i=(fLayerCount-1) then
begin
//出力層の場合
SetLength(back_error,Length(Outputs));
SUBPS(back_error[0],fOut[i][0],Outputs[0],Length(Outputs));
end
else
begin
//隠れ層(次の層への入力の偏微分係数)
//最後に追加された入力の勾配(layer_grads_x)をback_errorに入れる
SetLength(back_error,Length(layer_grads_x));
Move(
layer_grads_x[0],
back_error[0],
SizeOf(layer_grads_x[0])*Length(layer_grads_x)
);
end;
for j := Low(fSum[i]) to High(fSum[i]) do
begin
if i=(fLayerCount-1) then
begin
//出力層の場合
if fActivationFunc=TMamActivationFunc.Sigmoid then
//恒等関数の導関数
active_der:=1.0
else
//シグモイド関数の導関数
active_der:=SigmoidDerivative(fSum[i][j]);
end
else
begin
//出力層以外の場合
if fActivationFunc=TMamActivationFunc.Sigmoid then
//シグモイド関数の導関数
active_der:=SigmoidDerivative(fSum[i][j])
else
//ReLU関数の導関数
active_der:=ReLUDerivative(fSum[i][j]);
end;
//fOut[i-1]配列をsum_der_wにコピー
SetLength(sum_der_w,Length(fOut[i-1]));
Move(
fOut[i-1][0],
sum_der_w[0],
Sizeof(fOut[i-1][0])*Length(fOut[i-1])
);
sum_der_b:=1.0;
//fWeight[i-1][j]配列をsum_der_xにコピー
SetLength(sum_der_x,Length(fWeight[i-1][j]));
Move(
fWeight[i-1][j][0], sum_der_x[0],
Sizeof(fWeight[i-1][j][0])*Length(fWeight[i-1][j])
);
//勾配を計算
delta:=back_error[j]*active_der;
//勾配からバイアス計算してバイアスを更新する
fBias[i-1][j]:=fBias[i-1][j]-delta*sum_der_b*fLearningRate;
if j=0 then SetLength(layer_grads_x,Length(sum_der_w));
//勾配から重みの計算を行い重みを更新する
AVXcoffSum(
fWeight[i-1][j][0],sum_der_w[0],-delta*fLearningRate,Length(sum_der_w));
//入力は各ノードから前のノードに接続する全ての入力を合計する
if j=0 then
begin
Mul(layer_grads_x[0],sum_der_x[0],delta,Length(layer_grads_x));
end
else
begin
AVXcoffSum(
layer_grads_x[0],sum_der_x[0],delta,Length(sum_der_w));
end;
end;
end;
end;
constructor TMamAnn.Create(
NeuronCountInLayers:TArray<Integer>;LerningRate: Single=0.2;
ActivationFunc:TMamActivationFunc=TMamActivationFunc.Sigmoid);
var i,j,k,num:Integer;
scale:Single;
begin
fLearningRate:=LerningRate;
if fLearningRate>0.999 then fLearningRate:=0.999;
if fLearningRate<0.001 then fLearningRate:=0.001;
//Sigmoid または ReLU
fActivationFunc:=ActivationFunc;
fLoss:=0;
fTrainCount:=0;
fLayerCount:=Length(NeuronCountInLayers);
SetLength(fNeuronCountInLayers,fLayerCount);
Move(
NeuronCountInLayers[0],
fNeuronCountInLayers[0],
SizeOf(NeuronCountInLayers[0])*Length(NeuronCountInLayers)
);
Randomize;
//値初期化
SetLength(fOut,fLayerCount);
SetLength(fSum,fLayerCount);
for i := Low(fOut) to High(fOut) do
begin
num:=fNeuronCountInLayers[i];
SetLength(fOut[i],num);
SetLength(fSum[i],num);
end;
//バイアス初期化(0にする)
SetLength(fBias,fLayerCount-1);
for i := Low(fBias) to High(fBias) do
begin
SetLength(fBias[i],fNeuronCountInLayers[i+1]);
for j := Low(fBias[i]) to High(fBias[i]) do
fBias[i][j]:=0;
end;
//重みづけ初期化
SetLength(fWeight,fLayerCount-1);
for i := Low(fWeight) to High(fWeight) do
begin
SetLength(fWeight[i],fNeuronCountInLayers[i+1]);
for j := Low(fWeight[i]) to High(fWeight[i]) do
begin
SetLength(fWeight[i][j],Length(fOut[i]));
if i=High(fWeight) then
begin
scale:=1/sqrt(Length(fWeight[i][j]));
end
else
begin
//乱数だけだと永遠にMSEが収束しない場合がある(1/20回くらい)
if fActivationFunc=TMamActivationFunc.Sigmoid then
//平均0、1/√nのガウス分布乱数
scale:=1/sqrt(Length(fWeight[i][j]))
else
//平均0、√(2/(n1+n2))のガウス分布乱数
scale:=sqrt(2/Length(fWeight[i][j]))
end;
for k := Low(fWeight[i][j]) to High(fWeight[i][j]) do
begin
if (fActivationFunc=TMamActivationFunc.Sigmoid) then
begin
if k=Low(fWeight[i][j]) then
fWeight[i][j][k]:=scale
else if k=High(fWeight[i][j]) then
fWeight[i][j][k]:=-scale
else
fWeight[i][j][k]:=RandG(0,scale);
end
else
begin
if (i=High(fWeight[i])) then
begin
if k=Low(fWeight[i][j]) then
fWeight[i][j][k]:=scale
else if k=High(fWeight[i][j]) then
fWeight[i][j][k]:=-scale
else
fWeight[i][j][k]:=RandG(0,scale);
end
else
if k=Low(fWeight[i][j]) then
fWeight[i][j][k]:=scale*3.5
else if k=High(fWeight[i][j]) then
fWeight[i][j][k]:=-scale*0.5
else
fWeight[i][j][k]:=RandG(0,scale);
end;
end;
end;
end;
end;
constructor TMamAnn.Create(Filename: String);
begin
Randomize;
Self.LoadFromFile(Filename);
end;
destructor TMamAnn.Destroy;
begin
inherited;
end;
procedure TMamAnn.ForwardProp(Inputs: TArray<Single>);
var i,j{,k}:Integer;
ww:Single;
begin //順伝播
//入力層に入力値を入れる
Move(Inputs[0],fSum[0][0],SizeOf(Inputs[0])*Length(Inputs));
Move(Inputs[0],fOut[0][0],SizeOf(Inputs[0])*Length(Inputs));
//入力層から中間層から出力層まで計算する
for i := Low(fWeight) to High(fWeight) do
begin
for j := Low(fWeight[i]) to High(fWeight[i]) do
begin
//fSum[i+1][j]:=
// fOut[i][ 0]*fWeight[i][j][ 0]+
// fOut[i][ 1]*fWeight[i][j][ 1]+
// fOut[i][...]*fWeight[i][j][...]+fBias[i][j];
//fOut[i*1][j]:=活性化関数(fSum[i+1][j]);
ww:=fBias[i][j]+MulAdd(fOut[i][0],fWeight[i][j][0],Length(fOut[i]));
fSum[i+1][j]:=ww;
if i=(fLayerCount-2) then
begin
//出力層の場合
if fActivationFunc=TMamActivationFunc.Sigmoid then
begin
//恒等関数
//ww:=ww;
end
else
begin
//シグモイド関数
ww:=Sigmoid(ww);
end;
end
else
begin
//出力層以外の場合
if fActivationFunc=TMamActivationFunc.Sigmoid then
//シグモイド関数
ww:=Sigmoid(ww)
else
//ReLU関数
ww:=ReLU(ww);
end;
fOut[i+1][j]:=ww;
end;
end;
end;
function TMamAnn.GetLearningRate: Single;
begin
result:=fLearningRate;
end;
function TMamAnn.GetMSE: Single;
begin //MSE(平均二乗誤差)出力
if fTrainCount>0 then
result:=fLoss/fTrainCount
else
result:=0;
end;
procedure TMamAnn.LoadFromFile(FileName: String);
var strm:TMemoryStream;
i,j,k:Integer;
act:Integer;
begin //ファイルからの読み込み
strm:=TMemoryStream.Create;
try
strm.LoadFromFile(FileName);
strm.Position:=0;
//活性化関数読み込み
strm.ReadData(act);
if act=0 then
fActivationFunc:=TMamActivationFunc.Sigmoid
else
fActivationFunc:=TMamActivationFunc.ReLU;
//層数読み込み
strm.ReadData(fLayerCount);
//層ごとのニューロン数読み込み
setLength(fNeuronCountInLayers,fLayerCount);
for i := 0 to fLayerCount-1 do
strm.ReadData(fNeuronCountInLayers[i]);
//学習率の読み込み
strm.ReadData(fLearningRate);
//損失値(累計2乗誤差)読み込み
strm.ReadData(fLoss);
//学習回数読み込み
strm.ReadData(fTrainCount);
//fSum,fOutの準備
SetLength(fSum,fLayerCount);
SetLength(fOut,fLayerCount);
for i := 0 to fLayerCount-1 do
begin
SetLength(fSum[i],fNeuronCountInLayers[i]);
SetLength(fOut[i],fNeuronCountInLayers[i]);
end;
//バイアス読み込み
SetLength(fBias,fLayerCount-1);
for i := Low(fBias) to High(fBias) do
begin
SetLength(fBias[i],fNeuronCountInLayers[i+1]);
for j := Low(fBias[i]) to High(fBias[i]) do
begin
strm.ReadData(fBias[i][j]);
end;
end;
//重み読み込み
SetLength(fWeight,fLayerCount-1);
for i := Low(fWeight) to High(fWeight) do
begin
SetLength(fWeight[i],fNeuronCountInLayers[i+1]);
for j := Low(fWeight[i]) to High(fWeight[i]) do
begin
SetLength(fWeight[i][j],fNeuronCountInLayers[i]);
for k := Low(fWeight[i][j]) to High(fWeight[i][j]) do
begin
strm.ReadData(fWeight[i][j][k]);
end;
end;
end;
finally
strm.Free;
end;
end;
procedure TMamAnn.Run(Inputs: TArray<Single>; out Outputs: TArray<Single>);
begin //予測の実行
ForwardProp(Inputs);
//出力層の値のコピー
SetLength(Outputs,Length(fOut[High(fOut)]));
Move(
fOut[High(fOut)][0],
Outputs[0],
SizeOf(fOut[High(fOut)][0])*Length(fOut[High(fOut)])
);
end;
procedure TMamAnn.SaveToFile(FileName: String);
var strm:TMemoryStream;
i,j,k:Integer;
act:Integer;
begin //バイナリで保存する
strm:=TMemoryStream.Create();
try
//活性化関数保存
if fActivationFunc=TMamActivationFunc.Sigmoid then
act:=0
else
act:=1;
strm.WriteData(act);
//層数保存
strm.WriteData(fLayerCount);
//層ごとのニューロン数保存
for i := Low(fNeuronCountInLayers) to High(fNeuronCountInLayers) do
strm.WriteData(fNeuronCountInLayers[i]);
//学習率保存
strm.WriteData(fLearningRate);
//損失値(累計2乗誤差)保存
strm.WriteData(fLoss);
//学習回数保存
strm.WriteData(fTrainCount);
//バイアス保存
for i := Low(fBias) to High(fBias) do
for j := Low(fBias[i]) to High(fBias[i]) do
strm.WriteData(fBias[i][j]);
//重み保存
for i := Low(fWeight) to High(fWeight) do
for j := Low(fWeight[i]) to High(fWeight[i]) do
for k := Low(fWeight[i][j]) to High(fWeight[i][j]) do
strm.WriteData(fWeight[i][j][k]);
strm.SaveToFile(FileName);
finally
strm.Free;
end;
end;
procedure TMamAnn.SetLearningRate(LearningRage:Single);
begin
if LearningRate>0.999 then LearningRate:=0.999;
if LearningRate<0.001 then LearningRate:=0.001;
fLearningRate:=LearningRate;
end;
function TMamAnn.Sigmoid(x: Single): Single;
begin //シグモイド関数
result:=1.0/(1.0+system.exp(-x))
end;
function TMamAnn.SigmoidDerivative(x:single): single;
begin //シグモイド関数の微分関数
result:=Sigmoid(x);
result:=result*(1.0-result);
end;
procedure TMamAnn.Train(Inputs, Outputs: Tarray<Single>);
var j:Integer;
sub:Single;
begin //学習
//順伝播
ForwardProp(Inputs);
//逆伝播
BackProp(Outputs);
//MSE(平均二乗誤差)の為に累計2乗誤差計算
for j := Low(Outputs) to High(Outputs) do
begin
inc(fTrainCount);
sub:=fOut[High(fOut)][j]-Outputs[j];
fLoss:=fLoss+sub*sub;
end;
end;
end.
